How can air and water cause change or movement?

Sometimes science is a nice break from math!

For the next several days, students will learn about and be able to explain how air and water are sources of energy.

Today we discussed wind power:

Tomorrow we'll find out about water (hydroelectric) power:

Both wind and water (hydroelectric) power are renewable sources of energy.

A generator can be used to transfer kinetic energy from moving air and water into electrical energy:

 

For today's home learning, students will research advantages and disadvantages of wind power.  They will use this information for a language arts writing assignment.  We'll do the same for water (hydroelectric) power on Monday.

Math Confidence Strategies

Every so often, I hear from a parent that her/his student lacks confidence in math.  Fortunately, there are several remedies to this problem:

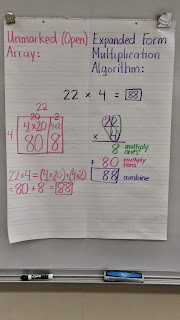
Fact fluency.  Being able to quickly recall sums, differences, products, and quotients frees up mental energy for multi-step skills and comprehending situations in which these skills can be used.  Reflex Math is a great tool for developing and maintaining fact fluency.  Your student's Reflex Math login information is in the front of her/his planner.  Our county's recommendation is at least three twenty-minute sessions weekly.  Some families have found it helpful to "schedule" three sessions per week on the family calendar. 

Knowing how to ask for help and seeing help.  Coming from someone who was extremely shy as a child and still struggles with a stubborn an introverted nature, this is much easier said than done.  Success can be found though, by taking baby steps.  First, help your student identify what specifically the student doesn't understand.  For example, is the student able to represent the situation with quick picture?  Does the student understand what a word problem is asking her/him to figure out or do?  Is s/he struggling to create an equation?  Does s/he know the first step towards solving the equation, or is another step the troublesome point?  Help your student formulate specific questions, and have her/him take ownership by writing them on a sticky note.  This will prepare your student to ask for help privately during Study Hall (8:00-8:25/2:35-2:50) or in class.  We all know how much better anything feels when we are prepared, especially when asking for help!

Talking math.  Spoken language naturally precedes written language.  How can we expect students to explain their thinking if they aren't able to communicate steps taken or correctly use vocabulary?  There are many ways students can talk math, from thinking aloud through problems while working on home learning to "playing school"--teaching a younger sibling, a parent, a pet, or even a stuffed animal what they are learning.

Hope this helps!

Multi-Digit Multiplication Strategies and Introducing Gizmos

With a short week, we're taking some time to practice multi-digit multiplication.  We're transitioning from using unmarked (open) arrays modeling partial products to using partial products with the expanded form multiplication algorithm.  We'll be working on 2 digit x 1 digit and 2 digit x 2 digit situations this week.  Over the next few weeks, we'll use the expanded form multiplication algorithm for 3 digit x 1 digit and 4 digit x 1 digit situations.  After Winter Break, we'll learn the U.S. standard multiplication algorithm for these situations.  So, until then, please be patient as your student develops greater number sense and is laying a solid foundation for better understanding and correctly using the U.S. standard multiplication algorithm.  :-)

Here's a video that shows how we have used an unmarked (open) array to model partial products.  Please ignore the last part about the standard algorithm for now.  :-)

This video will give you an idea of how to use the expanded form multiplication algorithm.  Honestly, I think the notation in this video is cluttery, so in class we think aloud most of the steps and just write the partial products , then combine them.  We've been using colored pencils to reinforce this when we practice:

We're also reviewing division with remainders this week.  One curriculum resource we're using is Gizmos.  Gizmos are online math and science simulations for third grade students and older.  Your student's Gizmo login information is in the front of her/his planner.  I added some math and science Gizmos from past units in case you would like your student to complete them for remediation or extra practice (or just for fun!).  By clicking on the "lesson info" link once you're logged in, you can print vocabulary sheets and student exploration packets like we use in class.  I recommend spending no longer than 30 minutes per session as most Gizmos contain multiple activities.  We're currently working on No Alien Left Behind (division and division with remainders).

Multiplication and Division as Inverse Operations

Students have been growing in their ability to multiply multi-digit numbers!  So far, we've been focusing on 2-digits X 1-digit situations, using unmarked arrays to model breaking apart one of the factors, multiplying each part, and combining the products (partial products strategy).

 

Equation: 3 x 45 = (40 x 3) + (5 x 3) = 120 + 15 = 135

 

On the division front, we're making progress in dividing larger 2-digit dividends by a 1-digit divisor using multiplication facts we know to get us there faster.  Last week, students were introduced to division with remainders and began learning how to interpret remainders, or decide what to do with the "extras" or "leftovers".  For example, leftover crackers can be divided into smaller fractional parts and shared; people cannot be divided this way, such as when arranging transportation to a destination.  Sometimes we just need to round up and get another vehicle, even though it won't be full.

This week, we'll continue investigating the inverse relationship between multiplication and division.  Here's a sneak preview!